Abstract
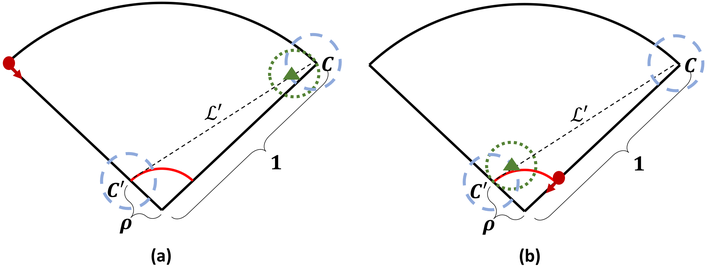
We consider a perimeter defense problem in a planar conical environment in which a single vehicle, having a finite capture radius, aims to defend a concentric perimeter from mobile intruders. The intruders are arbitrarily released at the circumference of the environment and move radially toward the perimeter with fixed speed. We present a competitive analysis approach to this problem by measuring the performance of multiple online algorithms for the vehicle against arbitrary inputs, relative to an optimal offline algorithm that has access to all future inputs. In particular, we first establish a necessary condition on the parameter space to guarantee finite competitiveness of any algorithm, and then characterize a parameter regime in which the competitive ratio is guaranteed to be at least 2 for any algorithm. We then design and analyze three online algorithms and characterize parameter regimes for which they have finite competitive ratios. Specifically, our first two algorithms are provably 1, and 2-competitive, respectively, whereas our third algorithm exhibits a finite competitive ratio that depends on the problem parameters. Finally, we provide numerous parameter space plots providing insights into the relative performance of our algorithms.