Abstract
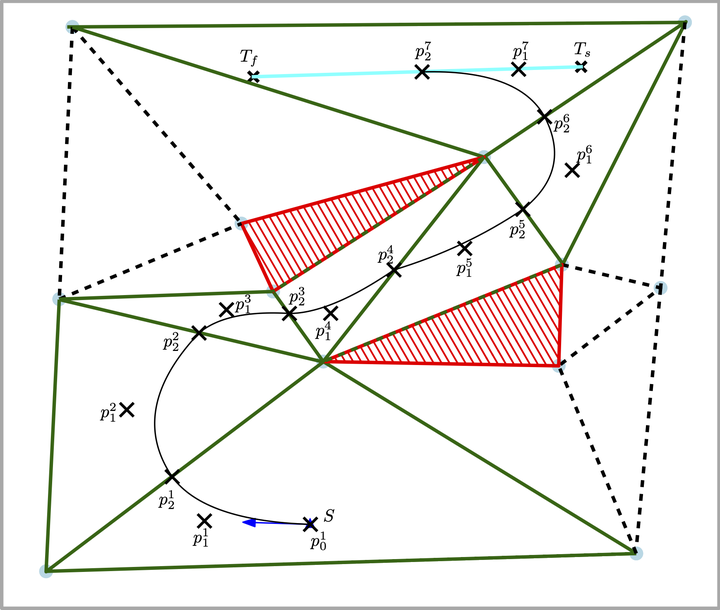
In this paper, we consider a trajectory planning problem where an autonomous vehicle aims to rendezvous with another cooperating vehicle in minimum time. The first vehicle has kinematic constraints, consequently feasible trajectories must have a maximum curvature less than a specified limit. Rendezvous is said to occur at the instant that the two vehicles are collocated with the same heading. We propose a technique to construct a trajectory, composed of piecewise quadratic Bézier curves, that satisfies the vehicle motion constraints and achieves rendezvous in minimum time. The methodology begins by finding safe flight corridors, which are constructed from sequences of triangles using constrained Delaunay triangulation of the feasible space; the triangles define the bounds of Bézier curves. We formulate the necessary constraints for continuity and feasibility as functions of the control points that define the Bézier curves, and the resulting optimization problem is solved using a nonlinear programming solver. The techniques developed were tested using simulated scenarios, and we present the results which highlight the efficacy of the proposed solution approach. Furthermore, the algorithm was implemented and tested in a field test and those results are presented.