The Synthesis of Optimal Control Laws Using Isaacs' Method for the Solution of Differential Games

Abstract

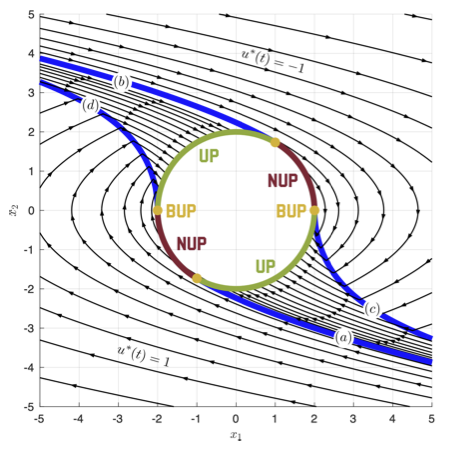
In this paper we advocate for Isaacs' method for the solution of differential games to be applied to the solution of optimal control problems. To make the argument, the vehicle employed is Pontryagin’s canonical optimal control example, which entails a double integrator plant. However, rather than controlling the state to the origin, we correctly require the end state to reach a terminal set that contains the origin in its interior. Indeed, in practice, it is required to control to a prescribed tolerance rather than reach a desired end state; achieving tight tolerances is expensive, and from a theoretical point of view, constraining the end state to a terminal manifold of co-dimension n-1 renders the optimal control problem well-posed. Thus, the `correct' solution of the optimal control problem is obtained. In this respect, two target sets are considered: a smooth circular target and a square target with corners; obviously, the size of the target sets can be shrunk to become very small. Closed-loop state-feedback control laws are developed which drive the double integrator plant from an arbitrary initial state to the target set in minimum time. This is accomplished using Isaacs' method for the solution of differential games, which entails Dynamic Programming (DP), working backward from the Usable Part (UP) of the target set, as opposed to obtaining the optimal trajectories using the necessary conditions provided by Pontryagin’s Maximum Principle (PMP). Special attention is given to the critical UP of the target set in the process of obtaining the global solution of the optimal control problem at hand. In this paper, Isaacs' method for the solution of differential games is applied to the solution of optimal control problems and the juxtaposition of the PMP and DP is undertaken.