Abstract
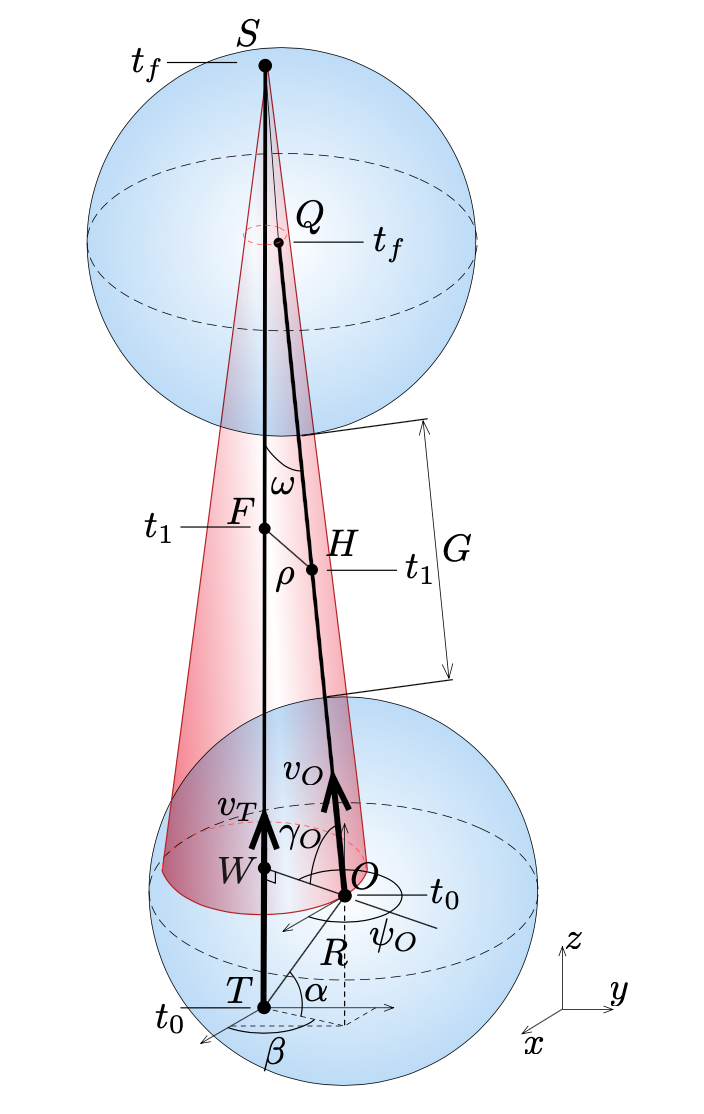
In this work, we consider a two-agent scenario consisting of an observer and non-maneuvering target. In the scenario, the observer is considered to be maneuverable and slower than the target. The observer is endowed with a nonzero radius of observation within which he strives at keeping the target for as long as possible. Using the calculus of variations, we pose and solve the optimal control problem, solving for the heading and flight path angle of the observer to maximize the amount of time the target vehicle is contained within his observation radius. Using the optimal observer heading and flight path angle, the exposure time is computed, based upon the initial azimuth and elevation by which the target is captured by the observer. The special cases, where the engagement may be represented in a plane, rather than 3-D, are also provided. Presented, along with examples, are the zero-time of exposure conditions, maximum exposure time conditions, and a proof that observation is persistent under the optimal observer strategy.