Abstract
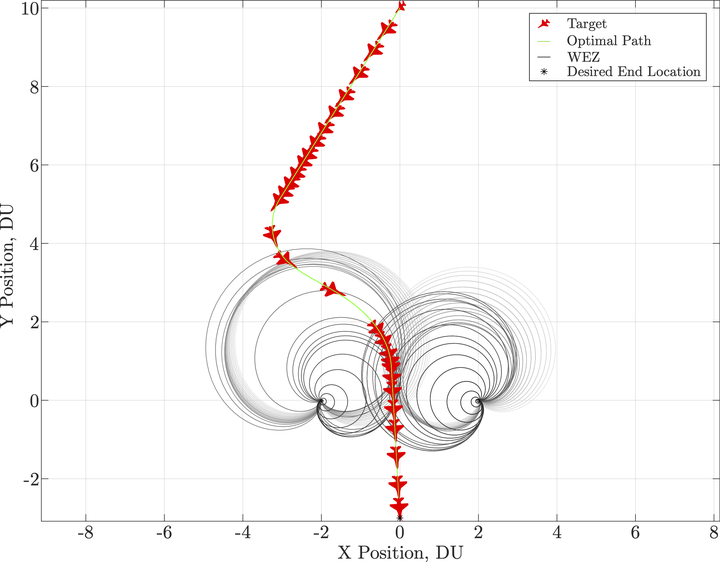
The work herein expresses an optimal control problem for an air vehicle to reach a desired location through two dynamic keep out zones. In today’s contested world, there are many instances where air vehicles are denied a portion of the airspace when trying to reach a desired target. Under these conditions the objective is to find the optimal route to the desired location while obeying path constraints. In this work, the path constraint is defined as the enemy’s ground weapon engagement zone, and is established in a way that simulates an anti-aircraft defense system. The vehicle’s objective is to reach the desired location in minimum time while completely avoiding the engagement zone. This optimal control problem is considered in the Cartesian plane, has a fixed final state, and free final time. The dynamics of the aircraft are a function of the aircraft’s velocity and heading. The velocity of the aircraft is assumed to be constant and the vehicle’s control is its heading rate. The engagement zone, which acts as a path constraint, is dynamic in that its effective range is a function of the engagement zone’s instantaneous line of sight angle and the aircraft’s instantaneous bearing angle. The desired final location is defined to be a point opposite the engagement zone from the aircraft’s initial location. Several scenarios are conducted to show path trajectories through multiple dynamic engagement zones. Results illustrate how aircraft dynamic maneuvers can minimize total flight time to a target while maintaining a safe distance from enemy threats. Further, while investigating multiple engagement zones, it is shown that an aircraft can maintain safe separation from multiple overlapping threats by manipulating relative bearing angles and the aircraft’s heading.